I parametri delle onde sonore
I parametri di un’onda sonora
Come abbiamo accennato in precedenza, la velocità di propagazione di un’onda sonora nonè fissa ma varia in relazione alle caratteristiche fisiche del mezzo in cui la propagazione
avviene. L’elasticità e la densità rappresentano le proprietà fisiche del mezzo di maggiore importanza per la propagazione. Per i gas la velocità di propagazione é data dalla seguente
relazione:
avviene. L’elasticità e la densità rappresentano le proprietà fisiche del mezzo di maggiore importanza per la propagazione. Per i gas la velocità di propagazione é data dalla seguente
relazione:
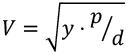
dove:
y = costante
p = pressione
d = densità
Come abbiamo accennato in precedenza, la velocità di propagazione di un’onda sonora non è fissa ma varia in relazione alle caratteristiche fisiche del mezzo di maggiore importanza per la propagazione. È da notare che la variazione della pressione atmosferica non influisce sulla velocità di propagazione nell’aria, mentre tale velocità dipende dalla temperatura secondo la relazione:

dove:
V0 = velocità a 0° centigradi
α = coefficiente di dilatazione termica
t = temperatura
Nella figura successiva è descritto il fenomeno della propagazione di un’onda sonora in vari mezzi.
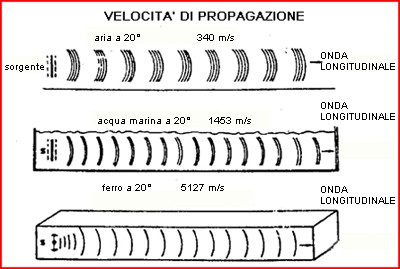
La velocità è maggiore nell’acqua rispetto all’aria. Infatti nell’acqua marina a 20° il suono viaggia percorrendo 1450 metri al secondo. Nei solidi, poi, la velocità del suono può raggiungere anche i 5000 metri al secondo come nel vetro e nel ferro. Vi sono due importanti parametri legati tra loro mediante la velocità di propagazione: essi sono la
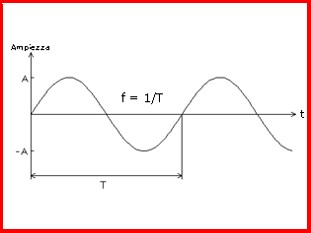
frequenza e la lunghezza d’onda. La frequenza f rappresenta il numero di oscillazioni sinusoidali che si compiono in un secondo. Periodo T= 1/f è allora il tempo in cui si compie una oscillazione sinusoidale completa. La frequenza, come è noto, si misura in Hertz.
frequenza e la lunghezza d’onda. La frequenza f rappresenta il numero di oscillazioni sinusoidali che si compiono in un secondo. Periodo T= 1/f è allora il tempo in cui si compie una oscillazione sinusoidale completa. La frequenza, come è noto, si misura in Hertz.
La lunghezza d’onda è lo spazio percorso nell’intervallo di tempo di un periodo dal fronte di propagazione dell’onda sonora. Immaginiamo di avere due sorgenti sonore che vibrino con la stessa frequenza e che agiscano una nell’aria e l’altra nell’acqua dando origine a due onde sonore. Nella propagazione in aria si osserva che, allorquando la cresta dell’onda contrassegnata con la lettera B giunge nel punto P, la cresta contrassegnata con la lettera A ha già percorso verso destra un certo spazio ed é giunta nel punto denominato R.
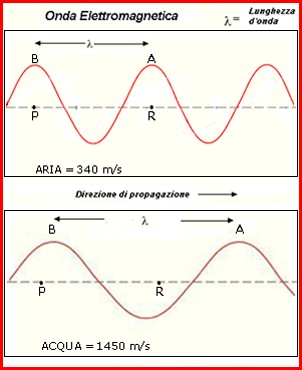
Si nota quindi che nell’intervallo di tempo pari a un periodo della frequenza di vibrazione della sorgente dell’onda sonora questa ha percorso lo spazio PR che prende il nome di lunghezza d’onda (λ); esso è uguale alla distanza che intercorre tra due creste successive di pressione dell’onda. È facile comprendere che la lunghezza d’onda sarà il prodotto della velocità del suono in un dato mezzo (u) per il periodo, ovvero il quoziente di questa velocità per la frequenza. La lunghezza d’onda dipende dal mezzo in cui si svolge la propagazione per onde. Infatti il suono che si propaga nell’acqua percorre, nell’intervallo di tempo pari ad
un periodo della frequenza di vibrazione della sorgente, uno spazio maggiore rispetto allo stesso suono che si propaga nell’aria. La velocità di propagazione di un suono entro un dato mezzo è pari al rapporto tra la lunghezza d’onda e il periodo della frequenza di vibrazione della sorgente.
un periodo della frequenza di vibrazione della sorgente, uno spazio maggiore rispetto allo stesso suono che si propaga nell’aria. La velocità di propagazione di un suono entro un dato mezzo è pari al rapporto tra la lunghezza d’onda e il periodo della frequenza di vibrazione della sorgente.

Abbiamo visto che il suono, come fenomeno fisico, é dato da una variazione di pressione in un mezzo elastico. Se nel mezzo non si verificano perturbazioni la pressione conserverà un
suo valore fisso, cioè la pressione sarà statica; nell’aria la pressione statica è rappresentata dalla pressione atmosferica. Se invece il mezzo elastico viene interessato da un fenomeno vibratorio si produrrà una pressione istantanea; essa è data dalla differenza tra la pressione esistente in un dato punto del mezzo e la pressione statica. Per misurare le variazioni di pressione dovremo considerare che esse sono forze che agiscono su delle superfici. L’unità di forza usata è il Newton per metro quadrato. Le variazioni di pressione legate al fenomeno sonoro vanno da 20 µNewton per metro quadrato fino a 63 Newton per metro quadrato. Per la misura della pressione istantanea (SPL), si è introdotta una scala logaritmica che consente di ovviare all’inconveniente dell’enorme divario di valori tra pressione minima e pressione massima. La scala esprime la relazione tra il minimo valore di pressione udibile, scelto come valore di riferimento, e il valore di pressione esistente in un punto dello spazio. Il valore che permette la minima sensazione di udibilità è di 20 µNewton per metro quadrato a 1000 Hertz, pari a 20 µPascal. (1 Pasca l= 1N per metro quadrato = 0.1µBar). L’intensità sonora è un’altra grandezza strettamente legata alla pressione; essa corrisponde al rapporto tra il valore quadratico della pressione con la densità del mezzo e la velocità di propagazione del suono nel mezzo stesso.
suo valore fisso, cioè la pressione sarà statica; nell’aria la pressione statica è rappresentata dalla pressione atmosferica. Se invece il mezzo elastico viene interessato da un fenomeno vibratorio si produrrà una pressione istantanea; essa è data dalla differenza tra la pressione esistente in un dato punto del mezzo e la pressione statica. Per misurare le variazioni di pressione dovremo considerare che esse sono forze che agiscono su delle superfici. L’unità di forza usata è il Newton per metro quadrato. Le variazioni di pressione legate al fenomeno sonoro vanno da 20 µNewton per metro quadrato fino a 63 Newton per metro quadrato. Per la misura della pressione istantanea (SPL), si è introdotta una scala logaritmica che consente di ovviare all’inconveniente dell’enorme divario di valori tra pressione minima e pressione massima. La scala esprime la relazione tra il minimo valore di pressione udibile, scelto come valore di riferimento, e il valore di pressione esistente in un punto dello spazio. Il valore che permette la minima sensazione di udibilità è di 20 µNewton per metro quadrato a 1000 Hertz, pari a 20 µPascal. (1 Pasca l= 1N per metro quadrato = 0.1µBar). L’intensità sonora è un’altra grandezza strettamente legata alla pressione; essa corrisponde al rapporto tra il valore quadratico della pressione con la densità del mezzo e la velocità di propagazione del suono nel mezzo stesso.


