L’audio digitale nasce, per il grande pubblico, all’inizio degli anni ’80, con l’introduzione del CD (Compact Disc). Con il passare degli anni esso ha preso sempre più piede nella produzione e post-produzione, audio e non solo. I suoi indiscutibili vantaggi per quanto riguarda la banda passante e il rapporto segnale/rumore hanno fatto sì che esso giungesse con una certa rapidità a occupare il vertice delle tecnologie audio. Attualmente l’audio digitale viene utilizzato praticamente in tutta la catena del segnale, da quando un suono entra nel mixer fino alla sua trasmissione o alla sua archiviazione su un opportuno supporto. È dunque indispensabile fornire almeno le basi necessarie a comprenderne il funzionamento, mentre per maggiori approfondimenti saranno necessarie ulteriori trattazioni a carattere monografico.

Un segnale audio digitale viene ottenuto dal segnale analogico mediante due operazioni fondamentali: il campionamento e la quantizzazione. Tale conversione viene effettuata da un convertitore analogico/digitale (A/D) che tiene conto di due parametri: la frequenza di campionamento e i bit per campione.
Secondo il Teorema del Campionamento di Nyquist - Shannon (o meglio di Whittaker - Nyquist - Kotelnikov - Shannon), ogni segnale analogico può essere trasformato in un segnale digitale senza perdere alcuna informazione, purchè la frequenza di campionamento sia almeno il doppio della sua ampiezza di banda.

Se definiamo f_c la frequenza di campionamento, f_c/2 è detta frequenza di Nyquist, e rappresenta il limite teorico utile per rappresentare in forma numerica un segnale analogico. Se il segnale analogico ha componenti di frequenza superiore alla frequenza di Nyquist si ha un degrado durante la fase di campionamento perché, a causa delle sovrapposizioni, tutte le componenti superiori vengono tagliate e ribattute a frequenza inferiore, comparendo nella banda come segnali fantasma (alias). Aumentando la frequenza di campionamento questo fenomeno, detto aliasing, scompare.

Pensiamo ora a un segnale musicale. Il nostro orecchio, come abbiamo avuto modo di analizzare in precedenza, è in grado di elaborare suoni aventi una frequenza massima non superiore ai 20 KHz. Stabilita la frequenza di Nyquist in 22.050 KHz, superiore quindi alla frequenza massima percepibile dall’orecchio umano, la frequenza di campionamento di 44.1 KHz (tipica del formato CD o PCM) dovrebbe assicurare una riproduzione ottimale della banda audio. In realtà questa scelta si è rivelata troppo bassa ed è stata la principale causa della difficoltà di ottenere da un Compact Disc un segnale audio di qualità. In origine la scelta fu dettata dal fatto che i primi registratori digitali utilizzavano come supporto un nastro video PAL o NTSC, e la frequenza di campionamento di 44.1 KHz era ottimale per la registrazione dei dati.
Successivamente fu introdotta per lo standard DAT la frequenza di campionamento di 48 KHz (la stessa utilizzata per il campionamento dell'audio legato a un contenuto video) e le cose migliorarono sensibilmente.
A questo punto sarà necessario trasformare queste letture (campioni o samples) in una sequenza di numeri (in inglese digits, da cui il termine digitale) 0 e 1. È adesso che entra in gioco la quantizzazione, che consiste nel determinare il valore di ogni campione. L'intervallo di variabilità del segnale (la cui ampiezza è determinata dalla frequenza di campionamento) viene diviso in intervalli uguali. Il numero di questi intervalli è determinato dal numero dei bit che si utilizzano per codificare ogni campione.

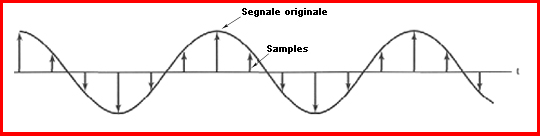
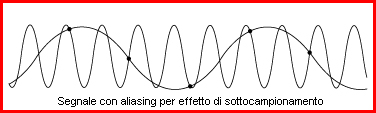
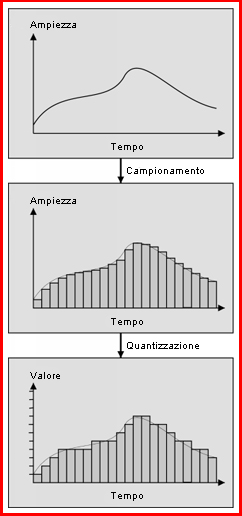
Lo standard CD prevede una quantizzazione a 16 bit. Questo significa che l’intervallo di variabilità del segnale viene suddiviso in 2¹⁶ = 65536 intervalli, quindi ognuno dei campioni può assumere un valore compreso tra 0 e 65535. Un formato a 24 bit, di contro, divide l’intervallo in 2²⁴ = 16777216 intervalli.
Il numero di bit utilizzati per la quantizzazione dipende essenzialmente da due fattori:

• la disponibilità e il costo di convertitori A/D adatti a trattare parole di questa lunghezza
• la quantità di memoria occupata dopo il campionamento

Anche se potessimo permetterci di immagazzinare il risultato di una quantizzazione a 64 bit dovremmo arrenderci di fronte all’impossibilità fisica di realizzare convertitori A/D di quella precisione. Tra l’altro, per ridurre il rumore termico, tutta l’apparecchiatura (e anche gli ascoltatori, se è per questo) dovrebbero essere mantenuti a una temperatura prossima allo zero assoluto.
È evidente, a questo punto, che sia il processo di campionamento che quello di quantizzazione introducono degli errori, i quali rivestono un’importanza fondamentale nella qualità del segnale finale. La qual cosa si può così sintetizzare:

• Più alta è la profondità di quantizzazione, minore è la potenza totale del rumore digitale.
• Più alta è la frequenza di campionamento, più il rumore si distribuisce alle alte frequenze. Il rumore che si trova fuori della banda audio può venire eliminato in un secondo tempo ed è ininfluente durante l’ascolto.
• In genere il rumore digitale è correlato con il segnale.

Fortunatamente, con la tecnologia digitale è relativamente facile trovare soluzioni economiche a questi problemi.

• Usare 24 bit invece che 16 porta i livelli di rumore digitale sotto l’inevitabile rumore termico dei componenti elettronici e li rende trascurabili (o per lo meno sposta il problema nella costruzione dei convertitori A/D di alta qualità).
• Effettuare il campionamento ad una frequenza più elevata di quella finale permette di filtrare via buona parte del rumore di quantizzazione (conversione A/D con oversampling).
• Per scorrelare il rumore dal segnale basta introdurre una perturbazione casuale e di bassissimo livello al momento della quantizzazione (aggiunta di dither o dithering)
• La matematica pone dei vincoli alla potenza totale di rumore associata con un determinato livello di quantizzazione, è però possibile alterare la distribuzione del rumore spostandolo verso le alte frequenze, dove l’orecchio umano è meno sensibile, e quindi rendendolo meno udibile (noise shaping). Questa operazione è molto più efficace se viene associata all’oversampling (sovracampionamento), in quanto gran parte del rumore esce così dalla banda audio.

Una volta ottenuto il segnale digitale, questo potrà essere memorizzato ed eventualmente elaborato, ma prima o poi sorgerà il problema di ascoltarlo. Per fare questo sarà necessario trasformare nuovamente il segnale digitale in analogico prima della fase di amplificazione di potenza.
Un singolo campione digitale è, come abbiamo visto, un numero; per trasformarlo in un segnale continuo, è possibile associare a esso un impulso rettangolare di durata determinata e di altezza pari al suo valore. Questa operazione, detta Sample & Hold, dal punto di vista matematico è una operazione di interpolazione che ha una sua ben precisa risposta in frequenza.
Quasi ogni tecnica di conversione D/A può essere schematizzata nel modo seguente:

1. pre-processing digitale
2. interpolazione Sample&Hold
3. post-processing analogico

Tutto ciò è valido dal punto di vista matematico, anche se, nella pratica, esistono differenti tipi di implementazione che potranno essere oggetto di una successiva, più approfondita trattazione.
Per concludere questa semplice introduzione all’audio digitale, possiamo sintetizzare che elevate frequenze di campionamento (es. 96 KHz), anche se non servono a riprodurre segnali a frequenza superiore a 20 KHz (comunque non udibili dall’uomo), consentono di ridurre le interferenze di tipo matematico nelle fasi di campionamento, quantizzazione e ricostruzione, nonché di semplificare i circuiti di conversione.
Mentre bisogna notare che non c’è una correlazione precisa tra i bit effettivi (che rappresentano una possibile misura del rumore complessivo) e la qualità del CD player stesso (valutata in termini di qualità sonora); bisogna anche sottolineare che, essendo il segnale di partenza a 44.1 KHz/16 bit, tutte le tecniche disponibili non possono introdurre una maggiore informazione ma permettono certamente di sfruttare quasi completamente l’informazione disponibile.